Back
PDF Version (113 KB)

Precedence
osurs@bluewin.ch    Urs Oswald    http://www.ursoswald.ch
September 23, 2002




Why Are the Mediation Points Where They Are?



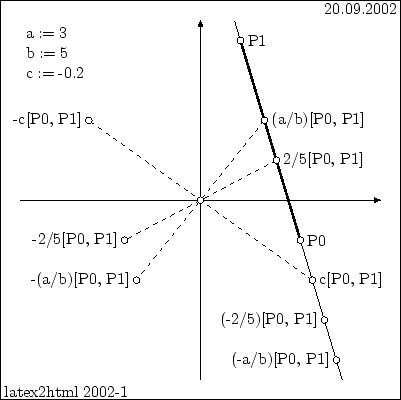
\includegraphics{Precedence1.eps}



For MetaPost, `2/5' is a $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$. As a consequence, `2/5[P0, P1]' is equivalent to `(2/5)[P0, P1]'. Furthermore, the figure above reveals that MetaPost reads `-2/5[P0, P1]' as `-((2/5)[P0, P1])'. Therefore, `-2/5[P0, P1]' is equivalent to `2/5[P0, P1] rotated 180'. And `-c[P0, P1]' is, for MetaPost, equivalent to '-(c[P0, P1])', which in turn is equivalent to `c[P0, P1] rotated 180'.
In order to understand how MetaFont processes the input, one has to understand two things:

  • how MetaPost breaks down the input into basic sequences called tokens,
  • how MetaPost groups these tokens to expressions.


Breaking Down the Input Into Tokens

An Experimental Approach

In order to find out how MetaPost breaks down an input sequence like

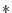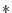  • sqrt3.142/2.718[(4, 7), 5.2(cosd45, sind45)]$\mathbf{\ast}$(1+2.5$\mathbf{\ast}$1.732),
write a file test.mp consisting of just one line, namely
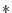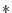  • ..sqrt3.142/2.718[(4, 7), 5.2(cosd45, sind45)]$\mathbf{\ast}$(1+2.5$\mathbf{\ast}$1.732).
Then start MetaPost: mpost test (or, depending on the system, mp test), and answer each `?' of MetaPost with `1'. This causes MetaPost to read the input line token by token. (You exit by entering `x'.)
In the case of the above input sequence, you will find that it is broken down into the tokens
\fbox{\rule[-.25em]{0em}{1.1em}sqrt}     \fbox{\rule[-.25em]{0em}{1.1em}3.142}     \fbox{\rule[-.25em]{0em}{1.1em}/}     \fbox{\rule[-.25em]{0em}{1.1em}2.718}     \fbox{\rule[-.25em]{0em}{1.1em}[}     \fbox{\rule[-.25em]{0em}{1.1em}(}     \fbox{\rule[-.25em]{0em}{1.1em}4}     \fbox{\rule[-.25em]{0em}{1.1em},}     \fbox{\rule[-.25em]{0em}{1.1em}7}     \fbox{\rule[-.25em]{0em}{1.1em})}     \fbox{\rule[-.25em]{0em}{1.1em},}     \fbox{\rule[-.25em]{0em}{1.1em}5.2}     \fbox{\rule[-.25em]{0em}{1.1em}(}     \fbox{\rule[-.25em]{0em}{1.1em}cosd}
\fbox{\rule[-.25em]{0em}{1.1em}45}     \fbox{\rule[-.25em]{0em}{1.1em},}     \fbox{\rule[-.25em]{0em}{1.1em}sind}     \fbox{\rule[-.25em]{0em}{1.1em}45}     \fbox{\rule[-.25em]{0em}{1.1em})}     \fbox{\rule[-.25em]{0em}{1.1em}]}     \fbox{\rule[-.25em]{0em}{1.1em}$\mathbf{\ast}$}     \fbox{\rule[-.25em]{0em}{1.1em}(}     \fbox{\rule[-.25em]{0em}{1.1em}1}     \fbox{\rule[-.25em]{0em}{1.1em}+}     \fbox{\rule[-.25em]{0em}{1.1em}2.5}     \fbox{\rule[-.25em]{0em}{1.1em}$\mathbf{\ast}$}     \fbox{\rule[-.25em]{0em}{1.1em}1.732}     \fbox{\rule[-.25em]{0em}{1.1em})}.


Three Kinds of Tokens

MetaPost knows three kinds of tokens:

  • numeric tokens,
  • string tokens,
  • symbolic tokens.
In the above example, the tokens
\fbox{\rule[-.25em]{0em}{1.1em}3.142}     \fbox{\rule[-.25em]{0em}{1.1em}2.718}     \fbox{\rule[-.25em]{0em}{1.1em}4}     \fbox{\rule[-.25em]{0em}{1.1em}7}     \fbox{\rule[-.25em]{0em}{1.1em}5.2}     \fbox{\rule[-.25em]{0em}{1.1em}45}     \fbox{\rule[-.25em]{0em}{1.1em}45}     \fbox{\rule[-.25em]{0em}{1.1em}1}     \fbox{\rule[-.25em]{0em}{1.1em}2.5}     \fbox{\rule[-.25em]{0em}{1.1em}1.732}    
are numeric, all the others are symbolic. The exact rules of how input is broken down into tokens can be found in KNUTH[2] or HOBBY[1]

What is or is not a numeric token is defined by the following set of syntactic rules:

$\mathnormal{\langle}$decimal digit $\mathnormal{\rangle}$ $\longrightarrow$0$\,\,\vert\,\,$1$\,\,\vert\,\,$2$\,\,\vert\,\,$3$\,\,\vert\,\,$4$\,\,\vert\,\,$5$\,\,\vert\,\,$6$\,\,\vert\,\,$7$\,\,\vert\,\,$8$\,\,\vert\,\,$9 (A)
$\mathnormal{\langle}$digit string $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$decimal digit $\mathnormal{\rangle}$$\,\,\vert\,\,$ $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$ $\mathnormal{\langle}$decimal digit $\mathnormal{\rangle}$ (B)
$\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$$\,\,\vert\,\,$. $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$$\,\,\vert\,\,$ $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$. $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$ (C)
In order to prove that `1.4142' is a $\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$, one first establishes, by rule (A), that each of `1',`4',`2' is a $\mathnormal{\langle}$decimal digit $\mathnormal{\rangle}$. So by the first part of rule (B), `1' and `4' are also of expression type $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$. Using the second part of (B) thrice in a row, one proves that `4142' is a $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$. Finally, by the third part of rule (C) it follows that `1.4142' is a $\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$.
The notation used here and afterwards to formulate syntactic rules for expressions were introduced about 1960 by John Backus and Peter Naur. Rule (A) determines that a $\mathnormal{\langle}$decimal digit $\mathnormal{\rangle}$ is either of 0,1,2,3,4,5,6,7,8,9, and nothing else. Similarly, rule (C) determines that an expression is a $\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$ iff (if and only if) it is of one of the three following expression types: ` $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$', `. $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$', ` $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$. $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$'.
How can one prove that `.4.1' is not a $\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$? One has to prove that it is neither a $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$, nor of one of the two forms `. $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$' or ` $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$. $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$'. As a $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$ consists of decimal digits only, neither of `.4.1', `4.1', `.4' is a $\mathnormal{\langle}$digit string $\mathnormal{\rangle}$. So `.4.1' has none of the three possible forms of a $\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$.
For MetaPost, the input sequences `sqrt3a' and `sqrt 3a' are equivalent, as both are broken down into the tokens
\fbox{\rule[-.25em]{0em}{1.1em}sqrt}     \fbox{\rule[-.25em]{0em}{1.1em}3}     \fbox{\rule[-.25em]{0em}{1.1em}a},
and so are the input sequences `www.latex2html.org' and `www latex 2html org', both of which result in the sequence
\fbox{\rule[-.25em]{0em}{1.1em}www}     \fbox{\rule[-.25em]{0em}{1.1em}latex}     \fbox{\rule[-.25em]{0em}{1.1em}2}     \fbox{\rule[-.25em]{0em}{1.1em}html}     \fbox{\rule[-.25em]{0em}{1.1em}org}.
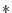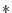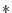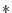And both of `sind30$\mathbf{\ast}$cosd60+sind60$\mathbf{\ast}$cosd30' and `sind 30 $\mathbf{\ast}$ cosd 60 + sind 60 $\mathbf{\ast}$ cosd 30' yield the token sequence
\fbox{\rule[-.25em]{0em}{1.1em}sind}     \fbox{\rule[-.25em]{0em}{1.1em}30}     \fbox{\rule[-.25em]{0em}{1.1em}$\mathbf{\ast}$}     \fbox{\rule[-.25em]{0em}{1.1em}cosd}     \fbox{\rule[-.25em]{0em}{1.1em}60}     \fbox{\rule[-.25em]{0em}{1.1em}+}     \fbox{\rule[-.25em]{0em}{1.1em}sind}     \fbox{\rule[-.25em]{0em}{1.1em}60}     \fbox{\rule[-.25em]{0em}{1.1em}$\mathbf{\ast}$}     \fbox{\rule[-.25em]{0em}{1.1em}cosd}     \fbox{\rule[-.25em]{0em}{1.1em}30}.

Numeric Expressions

The Complete Set of Syntactic Rules

The following diagram is taken from KNUTH[2], p. 211. It contains the complete and final set of syntactic rules for numeric expressions.

$\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$numeric variable $\mathnormal{\rangle}$ (1)
$\,\,\vert\,\,$ $\mathnormal{\langle}$numeric argument $\mathnormal{\rangle}$ (2)
$\,\,\vert\,\,$ $\mathnormal{\langle}$numeric token atom $\mathnormal{\rangle}$ (3)
$\,\,\vert\,\,$ $\mathnormal{\langle}$internal quantity $\mathnormal{\rangle}$ (4)
$\,\,\vert\,\,$normaldeviate (5)
$\,\,\vert\,\,$( $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$) (6)
$\,\,\vert\,\,$begingroup $\mathnormal{\langle}$statement list $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$ endgroup (7)
$\mathnormal{\langle}$numeric token atom $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$/ $\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$ (8)
$\,\,\vert\,\,$ $\mathnormal{\langle}$numeric token not followed by `/ $\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$' $\mathnormal{\rangle}$ (9)
$\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$ (10)
$\,\,\vert\,\,$ $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$[ $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$ , $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$] (11)
$\,\,\vert\,\,$length $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ (12)
$\,\,\vert\,\,$length $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$ (13)
$\,\,\vert\,\,$length $\mathnormal{\langle}$path primary $\mathnormal{\rangle}$ (14)
$\,\,\vert\,\,$length $\mathnormal{\langle}$string primary $\mathnormal{\rangle}$ (15)
$\,\,\vert\,\,$ASCII $\mathnormal{\langle}$string primary $\mathnormal{\rangle}$$\,\,\vert\,\,$oct $\mathnormal{\langle}$string primary $\mathnormal{\rangle}$$\,\,\vert\,\,$hex $\mathnormal{\langle}$string primary $\mathnormal{\rangle}$ (16)
$\,\,\vert\,\,$ $\mathnormal{\langle}$pair part $\mathnormal{\rangle}$ $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$ (17)
$\,\,\vert\,\,$ $\mathnormal{\langle}$transform part $\mathnormal{\rangle}$ $\mathnormal{\langle}$transform primary $\mathnormal{\rangle}$ (18)
$\,\,\vert\,\,$angle $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$ (19)
$\,\,\vert\,\,$turningnumber $\mathnormal{\langle}$path primary $\mathnormal{\rangle}$ (20)
$\,\,\vert\,\,$totalweight $\mathnormal{\langle}$picture primary $\mathnormal{\rangle}$ (21)
$\,\,\vert\,\,$ $\mathnormal{\langle}$numeric operator $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ (22)
$\,\,\vert\,\,$directiontime $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$ of $\mathnormal{\langle}$path primary $\mathnormal{\rangle}$ (23)
$\mathnormal{\langle}$pair part $\mathnormal{\rangle}$ $\longrightarrow$xpart$\,\,\vert\,\,$ypart (24)
$\mathnormal{\langle}$transform part $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$pair part $\mathnormal{\rangle}$ (25)
$\,\,\vert\,\,$xxpart$\,\,\vert\,\,$xypart$\,\,\vert\,\,$yxpart$\,\,\vert\,\,$yypart (26)
$\mathnormal{\langle}$numeric operator $\mathnormal{\rangle}$ $\longrightarrow$sqrt$\,\,\vert\,\,$sind$\,\,\vert\,\,$cosd$\,\,\vert\,\,$mlog$\,\,\vert\,\,$mexp (27)
$\,\,\vert\,\,$floor$\,\,\vert\,\,$uniformdeviate$\,\,\vert\,\,$ $\mathnormal{\langle}$scalar multiplication operator $\mathnormal{\rangle}$ (28)
$\mathnormal{\langle}$scalar multiplication operator $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$plus or minus $\mathnormal{\rangle}$ (29)
$\,\,\vert\,\,$ $\mathnormal{\langle}$numeric token atom not followed by + or - or a numeric token $\mathnormal{\rangle}$ (30)
$\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ (31)
$\,\,\vert\,\,$ $\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$ $\mathnormal{\langle}$times or over $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ (32)
$\mathnormal{\langle}$times or over $\mathnormal{\rangle}$ $\longrightarrow$*$\,\,\vert\,\,$/ (33)
$\mathnormal{\langle}$numeric tertiary $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$ (34)
$\,\,\vert\,\,$ $\mathnormal{\langle}$numeric tertiary $\mathnormal{\rangle}$ $\mathnormal{\langle}$plus or minus $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$ (35)
$\,\,\vert\,\,$ $\mathnormal{\langle}$numeric tertiary $\mathnormal{\rangle}$ $\mathnormal{\langle}$Pythagorean plus or minus $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$ (36)
$\mathnormal{\langle}$plus or minus $\mathnormal{\rangle}$ $\longrightarrow$+$\,\,\vert\,\,$- (37)
$\mathnormal{\langle}$Pythagorean plus or minus $\mathnormal{\rangle}$ $\longrightarrow$++$\,\,\vert\,\,$+-+ (38)
$\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$numeric tertiary $\mathnormal{\rangle}$ (39)

Some Consequences

The above set of rules implies:

  • Each $\mathnormal{\langle}$numeric token atom $\mathnormal{\rangle}$ is a $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$.        (1), (3)
  • Each $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$ is a $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$.        (10)
  • Each $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ is a $\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$.        (31)
  • Each $\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$ is a $\mathnormal{\langle}$numeric tertiary $\mathnormal{\rangle}$.        (34)
  • Each $\mathnormal{\langle}$numeric tertiary $\mathnormal{\rangle}$ is a $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$.        (39)

By lines 8 and 9, a $\mathnormal{\langle}$numeric token atom $\mathnormal{\rangle}$ is either a $\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$ or a $\mathnormal{\langle}$numeric token not followed by `/ $\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$' $\mathnormal{\rangle}$. So a $\mathnormal{\langle}$numeric token atom $\mathnormal{\rangle}$ is a $\mathnormal{\langle}$numeric token $\mathnormal{\rangle}$ or has one of the 9 forms

4/7 .693/7 3.14/7
4/.618 .693/.618 3.14/.618
4/2.718 .693/2.718 3.14/2.718

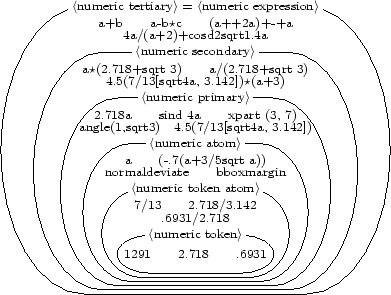
The figure below gives an overview of the subtypes of $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$. The classification of expressions is not absolute, but it depends on the context, as the following example shows. In the expression `.61803[2, 5]', the sequence `.61803' is a $\mathnormal{\langle}$numeric token atom $\mathnormal{\rangle}$; in the expression `.61803/3.14[2, 5]' it is not.

\includegraphics{Precedence3.eps}

Two Examples

Each one of the input sequences `sind4a', `sind 4 a', and `sind4.a' will result in the token sequence

\fbox{\rule[-.25em]{0em}{1.1em}sind}     \fbox{\rule[-.25em]{0em}{1.1em}4}     \fbox{\rule[-.25em]{0em}{1.1em}a}.
(The `d' in `sind' refers to degree, as `sind' expects the argument to be measured in degrees.) Let `a' be numeric. By line 27 of the set of syntactic rules for numeric expressions, the first token, \fbox{\rule[-.25em]{0em}{1.1em}sind}, is a $\mathnormal{\langle}$numeric operator $\mathnormal{\rangle}$. The second token is a $\mathnormal{\langle}$numeric token atom not followed by + or - or a numeric token $\mathnormal{\rangle}$. It is therefore, by line 30, a $\mathnormal{\langle}$scalar multiplication operator $\mathnormal{\rangle}$, and, by line 28, a $\mathnormal{\langle}$numeric operator $\mathnormal{\rangle}$. The third token is a $\mathnormal{\langle}$numeric variable $\mathnormal{\rangle}$ which is a $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$ by line 1 and a $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ by line 10. Therefore, the token sequence has the form
$\mathnormal{\langle}$numeric operator $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric operator $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$.
The only way of reducing this sequence is by line 22: $\mathnormal{\langle}$numeric operator $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ yields $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$, which means that `sind4a' is equivalent with `sind(4a)'. Again by use of line 22, we can finally reduce the sequence to $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$.
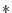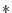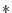The input sequence `sind4$\mathbf{\ast}$a' (or, equivalently, `sind 4 $\mathbf{\ast}$ a' or `sind 4$\mathbf{\ast}$a') has the form
sind $\mathnormal{\langle}$numeric token atom $\mathnormal{\rangle}$$\mathbf{\ast}$ $\mathnormal{\langle}$numeric variable $\mathnormal{\rangle}$,
and can therefore be converted by the syntax rules into
  • $\mathnormal{\langle}$numeric operator $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ $\mathnormal{\langle}$times or over $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$,
  • $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ $\mathnormal{\langle}$times or over $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$, (22)
  • $\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$ $\mathnormal{\langle}$times or over $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$, (31)
  • $\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$. (32)
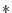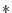The use of line 22 in the second step implies that `sind4$\mathbf{\ast}$a' is equivalent to `(sind4)$\mathbf{\ast}$a'.
It may seem arbitrary that this time, we do not classify the token \fbox{\rule[-.25em]{0em}{1.1em}4} as a $\mathnormal{\langle}$numeric token atom not followed by + or - or a numeric token $\mathnormal{\rangle}$, as we did in the previous example. Had we done so, we would have ended up with
$\mathnormal{\langle}$numeric operator $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric operator $\mathnormal{\rangle}$ $\mathnormal{\langle}$times or over $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$,
a sequence which cannot be proven to be a $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$ by the syntax rules.
While each $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ is also a $\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$, the reverse is not true. For the $\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$ `2*3.1415', we can prove that it is not a $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ by proving that it is of neither of the possible expression types given in lines 10 through 23: It is neither an isolated $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$ (10) nor a mediation expression (11), and interpreting the leading digit `2' as a $\mathnormal{\langle}$numeric operator $\mathnormal{\rangle}$ leads nowhere. It neither starts with a $\mathnormal{\langle}$pair part $\mathnormal{\rangle}$ nor a $\mathnormal{\langle}$transform part $\mathnormal{\rangle}$, and it does not begin with any of the remaining operators length, ASCII, oct, hex, angle, turningnumber, totalweight, directiontime ...of.

Syntax of Pair Expressions

The complete set of syntactic rules

The following diagram is taken from Donald E. Knuth, The METAFONTbook, p. 212:

$\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$pair variable $\mathnormal{\rangle}$ (40)
$\,\,\vert\,\,$ $\mathnormal{\langle}$pair argument $\mathnormal{\rangle}$ (41)
$\,\,\vert\,\,$( $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$ , $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$) (42)
$\,\,\vert\,\,$( $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$) (43)
$\,\,\vert\,\,$begingroup $\mathnormal{\langle}$statement list $\mathnormal{\rangle}$ $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$ endgroup (44)
$\,\,\vert\,\,$ $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$[ $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$ , $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$] (45)
$\,\,\vert\,\,$ $\mathnormal{\langle}$scalar multiplication operator $\mathnormal{\rangle}$ $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$ (46)
$\,\,\vert\,\,$point $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$ of $\mathnormal{\langle}$path primary $\mathnormal{\rangle}$ (47)
$\,\,\vert\,\,$precontrol $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$ of $\mathnormal{\langle}$path primary $\mathnormal{\rangle}$ (48)
$\,\,\vert\,\,$postcontrol $\mathnormal{\langle}$numeric expression $\mathnormal{\rangle}$ of $\mathnormal{\langle}$path primary $\mathnormal{\rangle}$ (49)
$\,\,\vert\,\,$penoffset $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$ of $\mathnormal{\langle}$pen primary $\mathnormal{\rangle}$ (50)
$\,\,\vert\,\,$penoffset $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$ of $\mathnormal{\langle}$future pen primary $\mathnormal{\rangle}$ (51)
$\mathnormal{\langle}$pair secondary $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$ (52)
$\,\,\vert\,\,$ $\mathnormal{\langle}$pair secondary $\mathnormal{\rangle}$ $\mathnormal{\langle}$times or over $\mathnormal{\rangle}$ $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ (53)
$\,\,\vert\,\,$ $\mathnormal{\langle}$numeric secondary $\mathnormal{\rangle}$* $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$ (54)
$\,\,\vert\,\,$ $\mathnormal{\langle}$pair secondary $\mathnormal{\rangle}$ $\mathnormal{\langle}$transformer $\mathnormal{\rangle}$ (55)
$\mathnormal{\langle}$transformer $\mathnormal{\rangle}$ $\longrightarrow$rotated $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ (56)
$\,\,\vert\,\,$scaled $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ (57)
$\,\,\vert\,\,$shifted $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$ (58)
$\,\,\vert\,\,$slanted $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ (59)
$\,\,\vert\,\,$transformed $\mathnormal{\langle}$transform primary $\mathnormal{\rangle}$ (60)
$\,\,\vert\,\,$xscaled $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ (61)
$\,\,\vert\,\,$yscaled $\mathnormal{\langle}$numeric primary $\mathnormal{\rangle}$ (62)
$\,\,\vert\,\,$zscaled $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$ (63)
$\mathnormal{\langle}$pair tertiary $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$pair secondary $\mathnormal{\rangle}$ (64)
$\,\,\vert\,\,$ $\mathnormal{\langle}$pair tertiary $\mathnormal{\rangle}$ $\mathnormal{\langle}$plus or minus $\mathnormal{\rangle}$ $\mathnormal{\langle}$pair secondary $\mathnormal{\rangle}$ (65)
$\,\,\vert\,\,$ $\mathnormal{\langle}$path tertiary $\mathnormal{\rangle}$intersectiontimes $\mathnormal{\langle}$path secondary $\mathnormal{\rangle}$ (66)
$\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$ $\longrightarrow$ $\mathnormal{\langle}$pair tertiary $\mathnormal{\rangle}$ (67)

Mediation Points

Now let's go back to the mediation expressions `2/5[P0, P1]' and `-2/5[P0, P1]'. (We suppose that a preliminary declaration pair P[] has been made.) The first is of the form

$\mathnormal{\langle}$numeric token atom $\mathnormal{\rangle}$[ $\mathnormal{\langle}$pair variable $\mathnormal{\rangle}$, $\mathnormal{\langle}$pair variable $\mathnormal{\rangle}$].
So we can establish each of the forms
  • $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$[ $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$, $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$],        (3), (40)
  • $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$[ $\mathnormal{\langle}$pair secondary $\mathnormal{\rangle}$, $\mathnormal{\langle}$pair secondary $\mathnormal{\rangle}$],        (52)
  • $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$[ $\mathnormal{\langle}$pair tertiary $\mathnormal{\rangle}$, $\mathnormal{\langle}$pair tertiary $\mathnormal{\rangle}$],        (64)
  • $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$[ $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$, $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$],        (67)
  • $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$. (45)
The only difference between the two sequences is the leading `-' in the second one. By lines 38 and 29, this `-' is a $\mathnormal{\langle}$plus or minus $\mathnormal{\rangle}$ and a $\mathnormal{\langle}$scalar multiplication operator $\mathnormal{\rangle}$. As the remaining sequence has been treated already in the first example, the second example reduces to

$\mathnormal{\langle}$scalar multiplication operator $\mathnormal{\rangle}$ $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$
and finally, by line 46, to $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$.
What about `a/b[P0, P1]'? This sequence is of the form

$\mathnormal{\langle}$numeric variable $\mathnormal{\rangle}$/ $\mathnormal{\langle}$numeric variable $\mathnormal{\rangle}$[ $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$, $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$]
and therefore
$\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$/ $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$[ $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$, $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$]
by line 1 of the syntax rules. There are no rules for reducing $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$/ $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$. So MetaPost tries by applying line 45 to $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$[ $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$, $\mathnormal{\langle}$pair expression $\mathnormal{\rangle}$], reducing this expression to $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$. But then it gets stuck with
$\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$/ $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$,
as it cannot divide a $\mathnormal{\langle}$numeric atom $\mathnormal{\rangle}$ by a $\mathnormal{\langle}$pair primary $\mathnormal{\rangle}$. The error message is:
! Not implemented: (known numeric)/(pair).

Bibliography

1
John D. Hobby, A User's Manual for MetaPost.
http://cm.bell-labs.com/who/hobby/
ftp://ftp.dante.de/tex-archive/info/epslatex.ps (784 KB)
ftp://ftp.dante.de/tex-archive/info/epslatex.pdf (1665 KB)

2
Donald E. Knuth. The METAFONTbook.
ADDISON-WESLEY, 1992, ISBN 0-201-13445-4 und ISBN 0-201-13444-6 (soft)